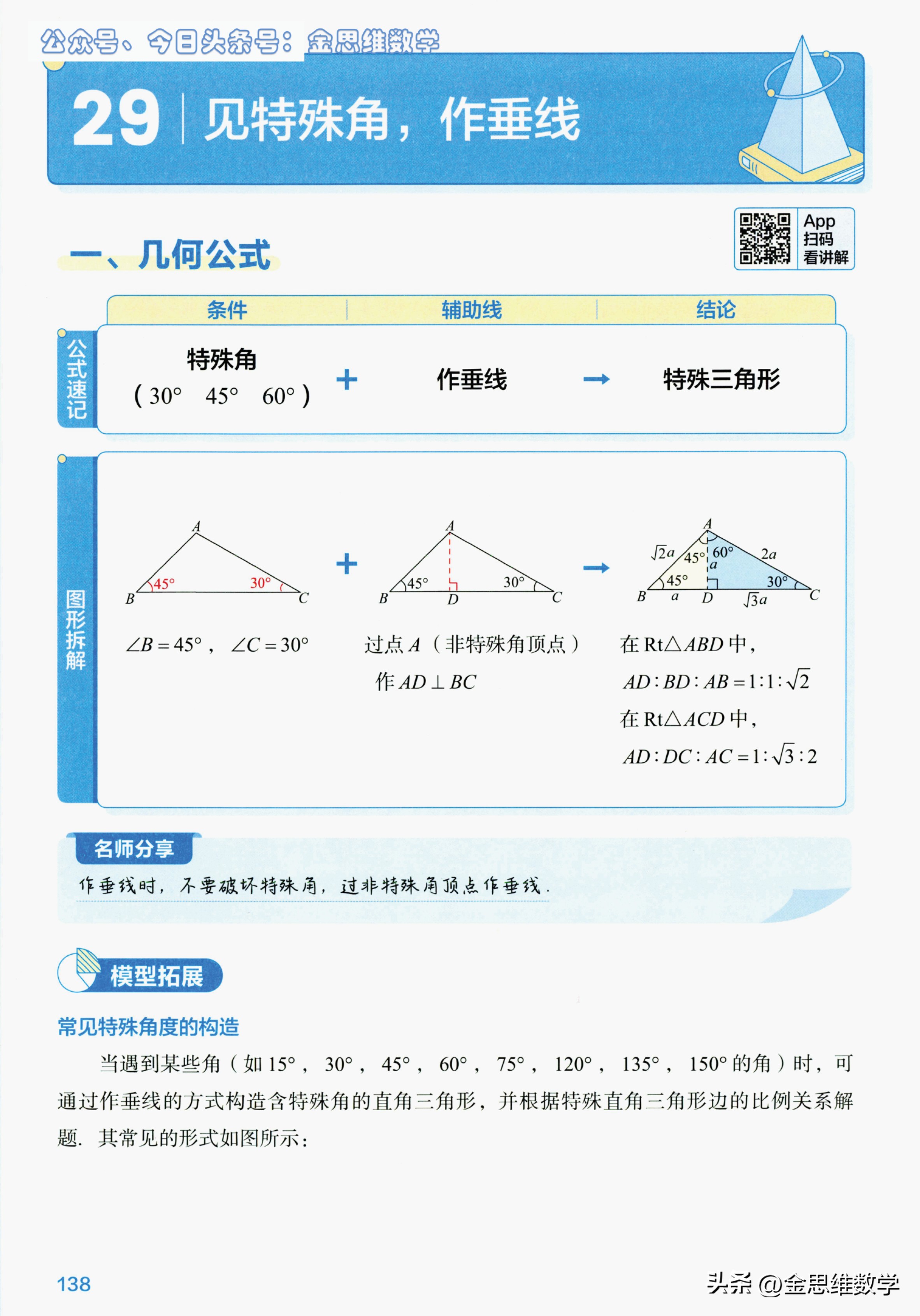
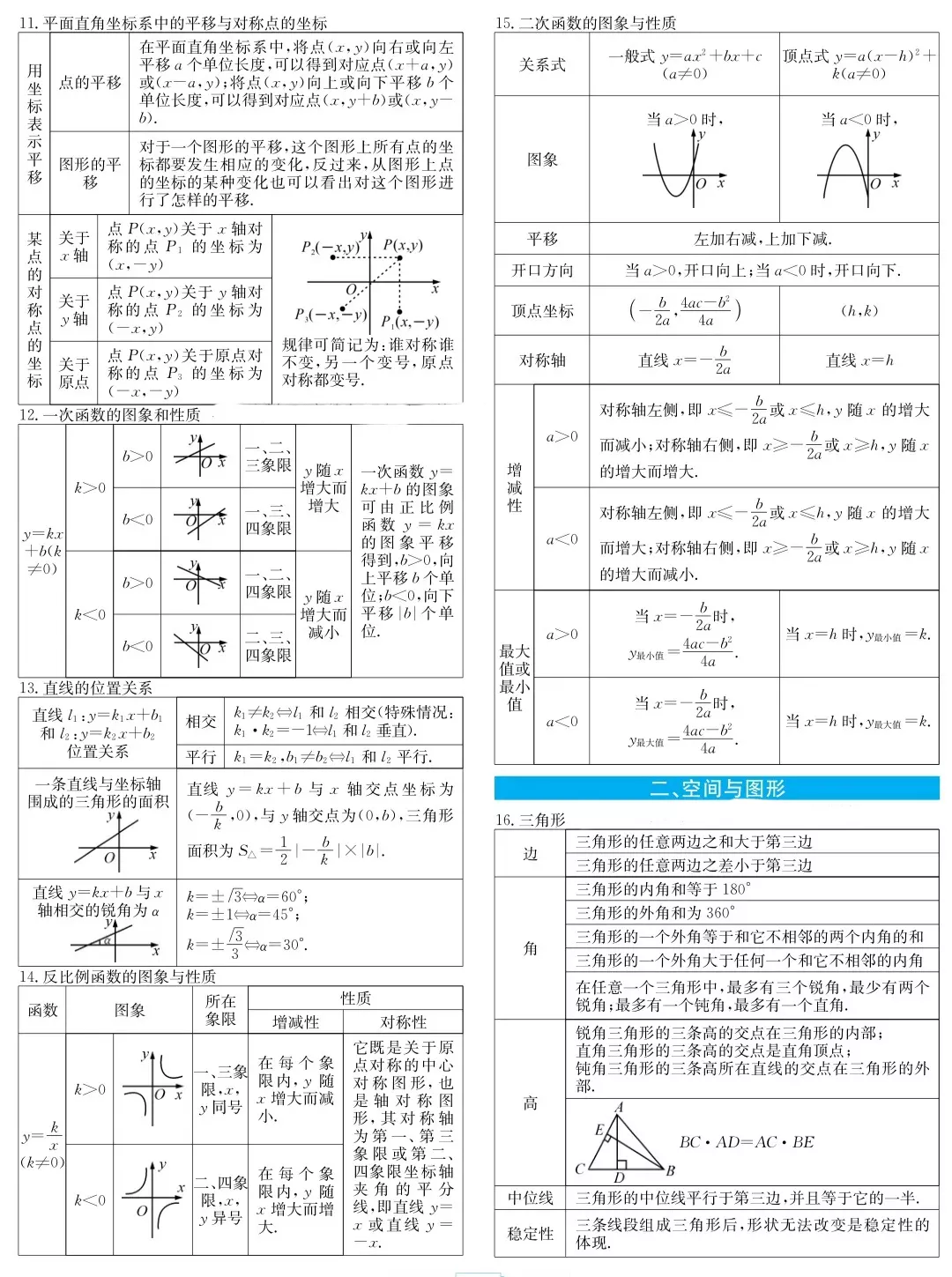
01
基本概念检验法
基本概念、法则、公式是同学们复习时最容易忽视的,因此在解题时极易发生概念性错误,所以,概念检验法是一种对症下药的方法。 如:下列函数中,是一次函数的有几个? (1)y=2x (2)y=ax+2 (3)y=3x-2 (4)y=2 答:有三个。错了,我们先来回想一下一次函数的定义:一切形如y=kx+b(k不等于0)的函数称为一次函数。对照定义形式,仅(1)和(3)为一次函数,而(2)的a可能为0,故只有两个。 02 对称原理检验法 对称的条件势必导致结论的对称(此结论通常被称为不充足理由律),利用这种对称原理可以对答案进行快速检验。 如:因式分解,(xy+1)(x+1)(y+1)+xy=(xy-y+1)(xy+x+1)结论显然错误。 左端关于x、y对称,所以右端也应关于x、y对称,正确答案应为:(xy+1)(x+1)(y+1)+xy=(xy+y+1)(xy+x+1)。 03 特殊情形检验法 问题的特殊情况往往比一般情况更易解决,因此通过特殊值、特例或极端状态来检验答案是非常快捷的方法,因为矛盾的普遍性寓于特殊性之中。 04 不变量检验法 某些数学问题在变化、变形过程中,其中有的量保持不变,如图形的平移、旋转、翻折时,图形的形状、大小不变,基本量也不变。利用这种变化过程中的不变量,可以直接验证某些答案的正确性。 05 等价关系检验法 等价关系不仅广泛用于解题时的等价转换,而且在检验答案时也可收到事半功倍的效果。 06 整体思想检验法 整体把握不仅能培养我们全局观念,养成良好的思维习惯,而且在检验答案时,通过彼此的遥相呼应、全局的和谐统一也可收到出奇制胜的效果。 07 逻辑推理检验法 答案的正确性不仅体现在与条件之间和谐而统一,而且不会导致逻辑矛盾,还会体现出规律性和数学美。这就给我们提供了检验答案的又一条新途径。 08 数形结合检验法 数是形的抽象概括,形是数的直观表现,数形结合相得益彰。 通过代数方法解出的问题,若能联想出几何背景,不妨用几何方法进行直观验证;用几何方法求出的答案,也可用代数方法进行精确验算。 09 一题多解检验法 多种解法比一种解法更使人放心,也更容易发现存在问题。 当一道题解完后,进行再思考,往往会闪出好念头,获得好方法,用新颖的方法再解后,有错则纠,无错则形成双保险。 10 直截了当检验法 直接检验法就是围绕原来的解题方法,针对求解的过程及相关结论进行核对、查校、验算等。 为配合检查,首先应正确使用草稿纸。建议大家将草稿纸叠出格痕,按顺序演算,并标上题号,方便检查对照。